Optical formulas

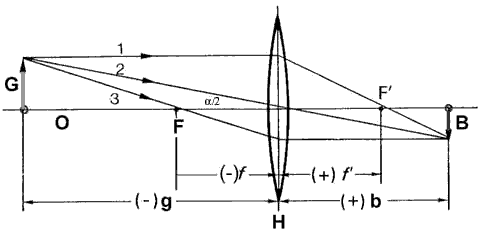
While photo lenses contain multiple lens elemens they can be viewed as a single optical element. The laws of geometric optics can be applied to a lens like they can be applied to a single element.

The following diagram shows how a point is projected by a converging lens onto its image. The lens lies on the optic center H perpendicular to the optic axis O. The two focal points F and F' are located left and right to the lens element at the distance f which is the focal length. The distance of the object from the optic center is the object distance g, and the distance of the image from the optic center is the image distance b. The photographic distance d is the distance between object and image, i. e. g+b.

Angle of view
Field of view
Magnification
Enlargement
Depth of field
Hyperfocal distance
Optical power
Focal length of lens with close-up lens
Magnification of lens with close-up lens
Calculator

Angle of view

The angle of view of a lens depends on its focal length and the size of the image. In lens makers' data sheets you most often find the diagonal angle of view. The formula to calculate the angle of view is

α = 2 × arctan(B / (2 × f))

using:

α: Angle of view
B: Image size
f: Focal length

If you derive a formula for f you will get:

f = B / (2 × tan(α / 2))

Sometimes the horizontal angle of view is given, or sometimes you like to calculate one angle from the other. The following formulas will help you with that:

Diagonal image size:   B = √( Bx² + By² )
Horizontal image size: B = Bx
Vertical image size:   B = By

using:

Bx: Horizontal image size
By: Vertical image size

Here are a few pre-calculated values:

Image format	diagonal	horizontal	vertical
35 mm	43 mm	36 mm	24 mm
6×4.5	69 mm	56 mm	41 mm
6×6	79 mm	56 mm	56 mm
6×7	86 mm	66 mm	56 mm

With these formulas it becomes clear why different focal lengths are considered “standard” for different image formats. If you calculate the angle of view from these focal lengths, you will get a value of about 50°. So what these different “standard” focal lengths have in common is a similar angle of view

Field of view

The field of view is the size (e. g. the width) of an object, filling a frame when photographed from a certain distance.

G = 2 × d × tan(α / 2)

using:

G: Field of view
d: Distance
α: Angle of view

Most often you're interested in the horizontal field of view, so:

α = α_hor

Magnification

The magnification is the relationship of the size of an object and the size of its image on film:

A = B / G

With 35 mm film, for example, a frame-filling image (36 mm wide) of a 36 mm wide object is said to be of the magnification 1. A smaller image has a magnification of less than 1. The value is usually given as a fraction, e. g. 1:1 instead of 1, or 1:2 instead of 0.5.

You can insert the formula for G into the above formula and thus can calculate magnification using focal length and distance. However, for close distances you will get incorrect values. This has the following reasons:

The formula for G is only an approximation for the real relationship and is only accurate enough for large distances (i. e. d >> f).
Many modern photo lenses use internal focusing, and with that the focal length changes with the focus distance. This effect is stronger for shorter distances. So f is actually smaller than its nominal value when you focus to shorter distances.

The calculator below makes accurate calculations.

Enlargement

The enlargement value is mostly given for binoculars and telescopes. It's simply the relationship between the field of view using binoculars and the field of view using the bare eye. The formula is:

V = G_f1 / G_f2

using:

G_f1: Field of view using a “standard” focal length
G_f2: Field of view using a “longer” focal length

Sometimes you want to calculate the enlargement also for telephoto lenses, e. g. to compare the enlarging effect of the lens with that of binoculars. When you insert the formula for G into the above formula, you will get the following simple result:

V = f2 / f1

using:

f1: “standard” focal length
f2: “longer” focal length

So for example, using a 400 mm lens on a 35 mm camera (with its “standard” focal length of 50 mm) will result in an 8 times enlargement, comparable to binoculars with 8× enlargement.

Depth of field

When you set up the camera to use a certain aperture and you focus to a given distance, there will be a range around the given distance that can be considered “in focus”. This distance range is the “depth of field” (or sometimes also called “depth of focus”). Depth of field depends on magnification and aperture. Magnification, as we've seen, depends on focal length and distance. The formulas to calculate the depth of field are as follows:

front DOF = c × F × d² / (f² + c × F × d)
rear  DOF = c × F × d² / (f² − c × F × d)

using:

c: Diameter of circle of confusion
F: Aperture number

The front DOF is the range in front of the object that is in focus, the rear DOF is the range behind the object that is in focus.

The parameter c is the diameter of the disc that is produced when a sharp dot of the object is out of focus and rendered as unsharp disc in the image. Discs smaller than c are considered “sharp enough” and hence “in focus”, discs larger than c are considered “not sharp enough” and hence “out of focus”. The circle of confusion is basically a threshold value for acceptable unsharpness. Technically, only the plane of focus is really sharp in an image, and everything before and behind the plane of focus is more or less unsharp. So the value of c is more or less arbitrary. If you are more critical with sharpness, c should be smaller, otherwise it can be larger. There is also considerable discussion if c should be chosen differently for different film formats. The proponents say that you will likely make smaller enlargements of larger film formats, and hence c should be bigger. The opponents say that DOF is only influenced by the lens, aperture and distance and not by the film format (see formula), and hence c should be constant.

Hyperfocal distance

When you set the focus distance to the hyperfocal distance with a given aperture, the depth of field will range from about half the hyperfocal distance to infinity. This is also the maximum depth of field for the given aperture. The formula for the hyperfocal distance is:

d_h + rear DOF = ∞

If you then insert the formula for rear DOF and isolate d_h you will get:

d_h = f² / (c × F)

Optical power

The optical power (unit: diopter) is reciprocal to the focal length (in meters), i. e.

D = 1 / f

This means a close-up lens with +2 dpt has a focal length of 500 mm.

Focal length of lens with close-up lens

A close-up lens (maybe in the form of reverse-mounted lens) changes the focal length of the combined lens system. The optical power of the close-up lens is added to the optical power of the base lens, i. e.

D_total = D_base + D_close-up

Converted to focal length, the formula is

1 / f_total = 1 / f_base + 1 / f_close-up
↔ f_total = 1 / (1 / f_base + D_close-up)

(with focal length in meters!)

If you prefer to use mm, add a factor of 1000:

f_total = 1000 / (1000 / f_base + D_close-up)

For example, a 100 mm lens with a +2 dpt close-up lens has a total focal length of 83 mm, i. e. it is reduced by the close-up lens.

But how does a smaller focal length result in a larger magnification? Well, the maximum extension of the lens is still unchanged. For example, if the above 100 mm lens has 1:1 magnification, it has 100 mm of extension. With the focal length reduced to 83 mm, maximum extension is now larger than the focal length, allowing it to focus closer and resulting in magnification larger than 1:1. So adding the close-up lens alone is not enough to increase magnification, you also have to get closer to the subject, and the close-up lens is just making this possible.

Magnification of lens with close-up lens

The magnification of a lens with a close-up lens is always the same when set to infinity. The formula is:

A = f_base / f_close-up
↔ A = f_base × D_close-up

Calculator

	horizontal	vertical	diagonal
Focal length (f)	mm
Distance (d)	m
Aperture
Object distance (g)	4.949 m
Image distance (b)	0.051 m
Circle of confusion (c)	mm
Depth of field	4.032 m–6.579 m (2.547 m)
Hyperfocal distance	20.83 m (10.42 m–∞)
Format
Image size (B)	23.5 mm	15.7 mm	28.26 mm
Field of view (G)	2.303 m	1.538 m	2.769 m
Angle of view (α)	26.45°	17.85°	31.56°
Magnification (B/G)	1:97.99 (0.01×)

Examples:

50 mm macro lens, focused by extension

Many lens makes offer such a lens, and many of them can focus up to 1:1 magnification. Focusing is purely by extension, i. e. the entire lens element package is moved forward. The spacing of the individual elements does not change.

With the calculator we can check the data in the lens' data sheet. We choose any film format and enter the focal length “50” and the distance “0.2” (the shortest possible distance of the lens). This results in a magnification of 1:1 as expected. We also see that the object distance and image distance are the same, and both are exactly half of the focus distance. The focal points of this system are 50 mm away from the optic center (hence “focal length”). Between the rear focal point and the image there's another 50 mm distance. This distance is the lens' extension. The focal length and the extension add up to the image distance. This confirms the rule of thumb that “with an extension as long as the focal length you will get a magnification of 1:1”.

100 mm macro lens with internal focusing

Many lens makers offer macro lenses with a longer focal length. These are, however, usually not focused by extension only, but internally (possibly by a combination of both). With this the lens elements move not only away from the film plane but move also relative to each other. The advantage is that you don't need as much of extension. The disadvantage is that the focal length is reduced when focusing at shorter distances.

Again we check the data in the data sheet of a lens. The focal length is 100 mm, and the shortest focus distance is 0.35 m. This is supposed to result in a magnification of 1:1. However, the above calculator displays a much larger value. This shows that at this distance the focal length is actually shorter than 100 mm. We can now reduce the focal length step by step until we get a magnification of 1:1. We will end up at a focal length of 87.5 mm. So this lens, focused at its shortest distance, has an actual focal length of 87.5 mm instead of 100 mm.

Please note that the resulting value is not exact using the above calculator. The value, however, indicates that indeed the true focal length is reduced, which is correct.

Readers' comments

#1: Comment posted by Markus Ziegler on June 5th, 2008 - 02:43:10 PM:
Hallo. Das ist eine Super wichtige Seite. Allerdings hätte ich gerne die möglichkeit gehabt, auch den zerstreuungskreis selbst einzustellen. tja, da sollte man programmieren können. der grund ist die diskussion über schärfenwahrnehmung bei digitalen (HD) medien. die soll nämlich anders sein, als beim klassischen film. Markus

#2: Comment posted by michael on August 30th, 2008 - 09:11:45 PM:
Danke für die Seite! Was ganz grossartig wäre, wenn es den Rechner für den MAC zum herunterladen gäbe, wenn ich mal nicht online bin. Das wäre ein tolles Tool. Michael

#3: Comment posted by scorp on September 29th, 2008 - 11:52:48 AM:
Gratulation zum Tiefenschärfe Rechner. Ich schließe mich michaels Wunsch nach einem Offline Rechner an. Auch eine Druckausgabe wäre Klasse. Beste Grüße

#4: Comment posted by Ovidiu on October 4th, 2008 - 12:39:30 PM:
Very useful info. Straight and well organized. Vielen Dank!

#5: Comment posted by corpore on October 13th, 2008 - 10:20:11 AM:
... großartige webside! Absolut nützlich...vielen Dank!! mfG corpore

#6: Comment posted by collin on April 2nd, 2009 - 07:18:25 AM:
very useful

#7: Comment posted by ralf on June 1st, 2009 - 05:38:50 PM:
Wie sieht das aus wenn ich einen Teleconverter verwende (z.B. 200 mm f/2.8 und 2-fach Teleconverter). Die Naheinstellgrenze sollte sich hierbei nicht ändern. Grüsse Ralf

Michael Hohner answers:
In dem Fall müssen alle Berechnungen mit Brennweite 400 mm und (maximal) Blende 5.6 erfolgen, an den anderen Parametern ändert sich nichts.

#8: Comment posted by tws on July 26th, 2009 - 06:09:38 PM:

Hallo, ich hätte da eine Frage die ich mit meinen eigenen Recherchen nicht herausbekommen habe. Ich bin eben nicht so der Pro. Folgende Situation. Kamera steht in 23m Entfernung von einer Skulptur (Steht auf dem Fussboden - die Kamera ist an der Decke installiert - also 2,30 vom Fussboden). Die Skulptur steht mittig zur Kamera und hat die Maße 2mbreit - 1,5 m hoch und eine Tiefe von 30cm. Welche Brennweite müsste ich nun min. benutzen um das Objekt formatfüllend aufs Bild zu bekommen. Meine Kameras`? 1. Sony mit 3CCD und 1/3" Sensor oder Canon mit 3CCD mit 1/2" Sensor. Bitte um Hilfe Stellung damit ich das endlich mal verstehe. Danke

Michael Hohner answers:

Mit dem obigen Rechner ist das einfach rauszufinden. Als Sensorgröße 1/3" auswählen, als Entfernung 23 m eingeben, und schon spuckt der Rechner bei 50 mm Brennweite ein Bildfeld (= Objektgröße) von 2.198 m × 1.649 m aus. Das kommt also hin. Bei 1/2"-Sensor muss die Brennweite entsprechend etwas länger sein, z.B. 70 mm (Bildfeld 2.09 m × 1.568 m). Die Montage an der Decke ist hier kaum relevant. Im Vergleich zur Aufnahme von der Raummitte und bei 23 m Entfernung ist der Winkel so spitz, dass die zusätzliche Entfernung kaum ins Gewicht fällt.

#9: Comment posted by Rick on January 29th, 2010 - 09:52:50 AM:
Hello, One correction.. You use: dh + rear DOF = ∞ This formula is meaningless. Infinity can not be used in algebraic equations. The only thing which 'adds' up to infinity, is infinity.

Michael Hohner answers:

I could change it to the more correct

d_h + rear DOF → ∞

but I don't think this would make it more understandable or change the practical application.

#10: Comment posted by Jan Madsen on March 22nd, 2010 - 06:42:41 PM:
Good site, but in the calculater the angle of view is not correct, except at infinity. It stays the same no matter what distance is plotted in, and for classic unit focusing lenses that is incorrect. The angle of view get narrower and narrower with closer distances ("breathing"), approximately half at 1:1, because the lens is now double as far from the sensor as at infinity.

Michael Hohner answers:
Such effects are not considered here, because the lens construction can not be entered and vary from lens design to lens design.

#11: Comment posted by Jörg Heeger on December 12th, 2011 - 05:18:25 PM:
Sehr geehrter Herr Hohner, vielen Dank, daß Sie Ihre Formelsammlung der Allgemeinheit zur Verfügung stellen. Ich beschäftige mich mit Videokameras und war froh, als ich Ihre Formeln fand. Beste Grüße Jörg Heeger aus Solingen

#12: Comment posted by Paul on March 22nd, 2012 - 10:29:00 AM:
Hallo, erstmal danke fuer die schoene Seite! Eine Frage/Bermerkung: Der Rechner fuer die Tiefenschaerfe verwendet die weiter oben angegebenen Formeln fuer T_v? Falls ja, dann sind die Berechnungen wohl nur fuer sehr kleine Abbildungsmassstaebe korrekt (wenn Entfernung und Gegenstandsweite praktisch uebereinstimmen) Gruesse, Paul

Michael Hohner answers:
Ja, der Rechner verwendet die obigen Formeln. Für größte Abbildungsmaßstäbe müsste man aber ein Objektiv als eine „dicke Linse” anstelle einer „dünnen Linse” modellieren, die dann zwei statt einer Hauptebene hat. Der Abstand der Hauptebenen ist aber für die meisten Objektive nicht bekannt (außer für den Hersteller), weswegen man an dieser Stelle steckenbleibt.

#13: Comment posted by Kavan Gujaratis on June 19th, 2012 - 09:09:53 PM:
Hello Mr. Michael, great website. So the FOV of a lens depends on the focal length of the lens, the distance between the object and the lens, the size of the frame...How about the diameter of the lens? I would think that the larger the diameter the larger the FOV....if not, why not? thanks, kavan

Michael Hohner answers:
FOV does not depend on the diameter of the lens, but on the size of the image. The image circle just needs to be large enough to illuminate the entire image.

#14: Comment posted by martin dechant on September 10th, 2012 - 08:46:02 PM:
Danke schoen, kann mich nur den anderen kommentaren anschliessen: ich finde die seite sehr praktisch! gute uebersicht, v.a. fuer mich als "nicht-optiker" essentiell! lg gautxori

#15: Comment posted by R.Gutzeit on December 16th, 2012 - 03:15:36 PM:
Hallo Super-Rechner ! ...jetzt fehlt nur noch ein 2. Rechner für die Berechnung der Helligkeit in Lumen. Was nützt mir die Tiefenschärfe bei Blende 4, wenn das Objektiv nur Blende 5,6 liefert ! Gibt es da eine Normkörnung wie bei Schleifpapier oder schläft die Foto-Branche seit 80 Jahren ... Gruß

Michael Hohner answers:
Der Rechner verwendet natürlich die geometrische Blende, die für die Schärfentiefeberechnungen entscheidend sind. Lichtverluste durch Reflexionen an den Linsenoberflächen sind kaum weiter zu reduzieren (die Vergütungen sind bereits sehr gut), und Verluste durch Auszug sind ebenfalls nicht zu vermeiden. Die Hersteller schlafen nicht, sie können nur die Physik nicht überlisten.

#16: Comment posted by Joergens.mi on December 26th, 2013 - 12:42:39 PM:
Schön wäre es noch, wenn man die Objektgröße eingeben könnte und dann die zur eingegebenen Brennweite passende Entfernung zur formatfüllenden Abbildung berechnet würde.

#17: Comment posted by Ed Chocolate on October 3rd, 2014 - 01:56:35 AM:
Great set of points here, clearly defined. Thanks.

#18: Comment posted by Wolfgang on March 22nd, 2015 - 06:00:40 PM:

Hallo! Kompliment für diese Seite und Ihr Wissen. Seit 3 Tagen versuche ich mir mit meinem "alten Kopf" (60 Jahre) aus Ihren Berechnungen und Formeln eine Tabelle zu bauen und kriege das einfach nicht hin. Mein Ziel: Ich habe 4 verschiedene, sich in der Brennweite überschneidende Zoom-Objektive und einen Zwischenring. Jetzt will ich herausfinden, bei welchem Abstand (nicht zu weit wegen der Verwacklungsgefahr, nicht zu dicht, um noch ausleuchten zu können) ich welches Objektiv nehmen soll. Priorität hat natürlich jeweils das Objektiv, bei dem ich den Zwischenring nicht benötige. Tja - und danach wollte ich die Tabelle dann noch mit den Ergebnissen erweitern, die sich herausstellen, wenn ich die Objektive in Retro-Stellung verwende - aber das wird wohl ein Ziel bleiben müssen - denke ich mal. Aber vielleicht ist ja auch dieses Vorhaben "einfach nur Mathematik"?! Haben Sie vielen lieben Dank und einen schönen Tag! Wolfgang

#19: Comment posted by Tom on April 16th, 2016 - 10:53:39 AM:
Danke, eine sehr schöne Seite. Als ich kürzlich mit meinem Neffen seine Kameramöglichkeiten durchrechnen wollte, stellten wir fest, dass beim Schärfentieferechner der 1/2.3 Sensor fehlt. Kann man den noch einbauen?

Michael Hohner answers:
Erledigt.

#20: Comment posted by om on April 23rd, 2016 - 02:37:41 PM:
I wish you had ray tracing sketches for every explanation and formula. It is a nightmare to relate forumalas with what you explain.

#21: Comment posted by Alex on May 23rd, 2016 - 01:34:15 PM:
Hallo Michael, tolle Formelsammlung, ganz großes Lob!!!!! Gibt es die auch als Excel-Sheet. Ich wäre dir sehr sehr dankbar. LG Alex

Michael Hohner answers:
Die Formelsammlung gibt es nicht in Excel.

#22: Comment posted by Aswan Korula on September 14th, 2016 - 04:47:49 PM:
I have a generic questions about combining two lenses....If I place two lenses (focal lengths f1 & f2) at a distance D apart, then I get their combined focal length (F) by the equation 1/F = 1/f1 + 1/f2 - D/(f1f2). My question is this....where is the optical centre of the combination?

#23: Comment posted by Hans Gruber on December 15th, 2020 - 09:06:53 AM:
Bei einem Objektiv sollte Auflagemaß theoretisch identisch mit der Bildweite sein. Bin in Mathematik/Physik/Optik nicht so gut. Kann es sein, daß im Objektiv eine Korrektur stattfindet, damit bei unterschiedlichen Brennweiten immer das gleiche Auflagemaß gewährleist wird? Läßt sich das verändern, z.B. damit ein 135mm-KB-Objektiv ein Auflagemaß von z.B. 100mm hat?

Michael Hohner answers:

Das Auflagemaß ist der Abstand zwischen Bildebene und Bajonett-Ebene. Wenn das identisch mit der Bildweite wäre, dann würde die Hauptachse immer auf der Bajonettebene liegen. Das ist offenbar nicht der Fall.

Das Bajonett (und damit das Auflagemaß) ist eigentlich kein Teil des optischen Systems. Es setzt lediglich mechanische Grenzen, d.h. normalerweise können die Linsen bei der Fokussierung nur vom Bajonett wegbewegt werden (Auszug), aber nicht zum Bajonett hin, und der Endanschlag der Fokusmechanik und das Auflagemaß sorgen für eine Unendlich-Fokussierung.

#24: Comment posted by Cher on January 5th, 2021 - 04:24:13 PM:

Hallo,

ich verwende eine digitale Systemkamera mit einem Vollformatsensor, also Kleinbild-Format. Das Objekt steht 4 Meter vor der Kamera und hat eine Größe von 2,29 Meter. Welche Brennweite darf ich höchstens verwenden, um das Objekt komplett abzubilden? Wie wird das berechnet? und wie ändert sich die die Brennweite, wenn ich statt eines digitalen Sensors einen analogen Kleinbildfilm verwende?

Michael Hohner answers:
Das ist am einfachsten mit dem Rechner oben zu ermitteln: als Format "35 mm" auswählen, und als Entfernung "4 m" eingeben. Dann mit der Brennweite spielen, bis sich als horizontale Objektgröße ca. 2,29 m ergibt. Das ist bei ca. 60 mm der Fall. Für analogen Film des gleichen Formats ändert sich dabei nichts.

#25: Comment posted by Matthias on June 2nd, 2023 - 06:12:41 AM:

Vielen Dank für die sehr lehrreiche Seite, die ich seit Jahren gerne und oft besuche! Der Rechner scheint in letzter Zeit allerdings einen Fehler zu haben, der die Objektgröße falsch ausgibt.

Wenn man z.B.Brennweite/Abstand von 50 und 0.2m eingibt, was korrekterweise einen Abbildungsmaß von 1:1 errechnet, stimmen Bild- und Objektgröße nicht überein. Die Objektgröße ist dann um den Faktor 4 zu groß.

Michael Hohner answers:
Danke für den Hinweis, der Fehler sollte jetzt korrigiert sein.

#26: Comment posted by Loredana on February 26th, 2024 - 12:41:40 PM:
I am trying to calculate: image size, field of view and angle of view using the formulas on this page. I obtain the correct results for all except for G (field of view). For example, with Hasselblad H3DII sensor + 60mm lens, distance 0.24m, the formula will be: G=20.24tan(49.42/2) giving a result of 0.22 which does not match 0.055m as results in the calculator, what am I doing wrong?

Michael Hohner answers:

There are a number of things at play here. First, in the formula for α there's "2f", while it should really be "b". Only at infinity focus b=2f. But the value of b (and consequently of g) is not really known unless you know the internal design of the lens. Second, a photo lens is not really a "thin lens" that is assumed for these formulas, it's a "thick lens". And third, many lenses are not precisely the focal length the maker claims. This all means that the closer you get to short distances/high magnification, the less accurate the results.

You can shoot a ruler with your camera and lens at 0.24 m and compare the object size with that given by the calculator. And then you can repeat with longer distances of several meters and see the differences.

Optical formulas

Contents

Angle of view

Field of view

Magnification

Enlargement

Depth of field

Hyperfocal distance

Optical power

Focal length of lens with close-up lens

Magnification of lens with close-up lens

Calculator

Examples:

50 mm macro lens, focused by extension

100 mm macro lens with internal focusing